Introdução
No artigo anterior foi destacado a teoria da adição binária, demonstrando na prática como os computadores realizam este tipo de operação aritmética utilizando circuitos lógicos. Além disso foi comentado que a partir da lógica de somador completo ou full adder, conseguimos construir circuitos digitais capazes de realizar outras operações, como no caso da subtração binária.
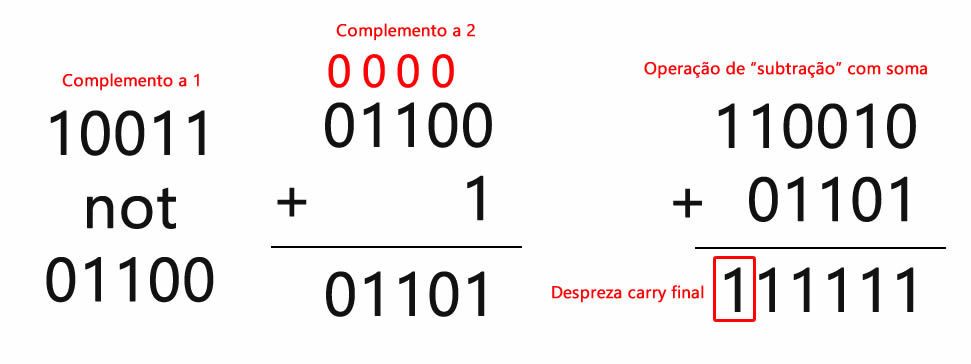
De um modo geral, esta operação decimal é feita a partir de dois números que queremos subtrair ou diminuir, como 50 - 19 = 31. A subtração binária segue as mesmas regras, seguindo o exemplo anterior, convertermos os dois números para a base binária, onde 50 é 110010 e 19 é 10011. Subtraindo esses dois números teremos 011111 ou 31.
Vamos detalhar passo a passo a operação binária abaixo no "papel", para isso devemos começar pelo bit menos significativo ou LSB, onde 10 - 1 = 1, este resultado possui emprestado um bit verdadeiro de seu vizinho esquerdo, sem este empréstimo chamado de bit de borrow não conseguimos realizar a operação. O próximo número do minuendo está falso, onde teremos que pegar emprestado do quarto bit verdadeiro (iniciando a contagem em zero pelo LSB), onde 10 - 1 = 1, o segundo e terceiro bit são falsos, eles também recebem um bit emprestado, sendo 1 - 0 = 1. Para os próximos minuendos aplica-se o bit de borrow, chegando no resultado de 011111.

Na prática os computadores não podem subtrair números binários, eles apenas sabem somar, mas isso não é um problema, desde que a subtração seja transformada em soma. Para ser ajustado à lógica computacional devemos utilizar o complemento a 2 para representar números com sinal (positivos e negativos). Um número binário positivo é representado de forma direta e um bit de sinal 0 é adicionado no bit mais significativo ou MSB, se o número binário é negativo, a magnitude é representada em forma de complemento a 2 e um bit de sinal em 1 é adicionado no MSB.

Utilizando o exemplo aritmético acima, vamos converter esta operação para um computador (Unidade Aritmética) calcular corretamente, o primeiro passo é converter o subtraendo para complemento a 1, onde 10011 será 01100, depois aplicamos o complemento a 2, onde 01100 + 1 = 01101 ou -19. Com este valor podemos realizar a "subtração" com soma, utilizando o minuendo 110010 (50) + 01101 (-19) = 111111, sempre desprezando o bit de carry final, onde teremos o resultado desejado.
Full Adder/Subtractor
Em uma abstração em baixo nível utilizando a eletrônica digital, podemos representar esta lógica utilizando full adders em conjunto com portas lógicas XOR. Relembrando o conceito, esta porta trabalha como uma lógica NOT controlada, e isso é interessante pois um full subtractor de 1 bit utiliza dois inversores em um full adder, porém para simplificar a lógica vamos fazer as operações de adição e subtração em paralelo com apenas dois circuitos integrados.
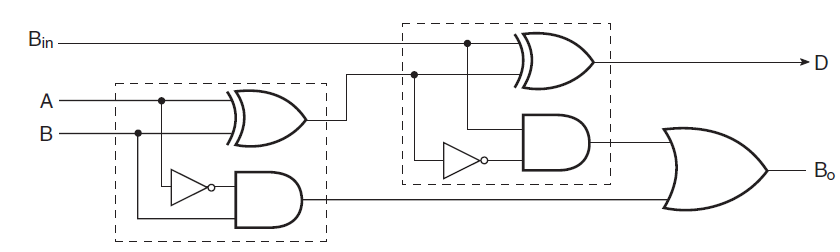
Utilizando um CI Full Adder de 4 bits como o CD4008 ou 74283, e um CI com 4 portas lógicas XOR de duas entradas como o CD4030 ou 7486, podemos desenvolver o nosso Full Adder/Subtractor e ver isso funcionando no protoboard. A lógica resumida deste circuito segue igual para o somador, porém cada entrada B do CI recebe a saída de uma XOR. Uma das entradas das XORs são interligadas com o CIN para receberem valores de 0V ou 5V via switch, representando as operações de adição ou subtração para o full adder.
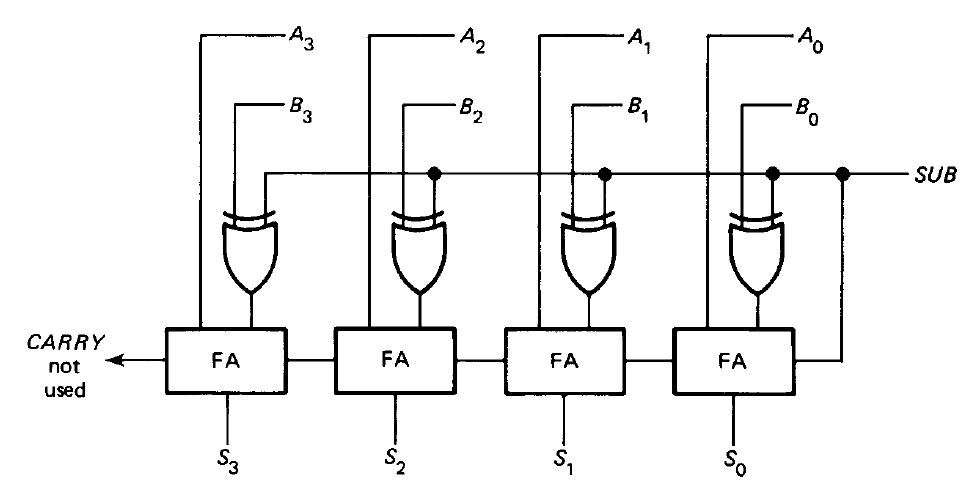
Após entender a teoria de funcionamento deste circuito, podemos iniciar a montagem no protoboard para visualizar estas operações digitais, para isso separe a lista de materiais necessários e siga o diagrama esquemático.
- 1 Protoboard
- 1 CI CD4008 ou 74283 (Full Adder 4 bits)
- 1 CI CD4030 ou 7486 (4 portas XOR de 2 entradas)
- 1 DIP switch de 8 vias ou 2 DIPs de 4 vias
- 1 Micro chave PCB de 2 posições
- 8 Resistores de 10K
- 5 Resistores de 1K
- 5 LEDs, de preferencia um LED com cor diferente para carry out
- 3 Capacitores de poliéster/cerâmico de 100nF
- Fios
- Fonte de alimentação 5V ou módulo fonte de alimentação para protoboard.
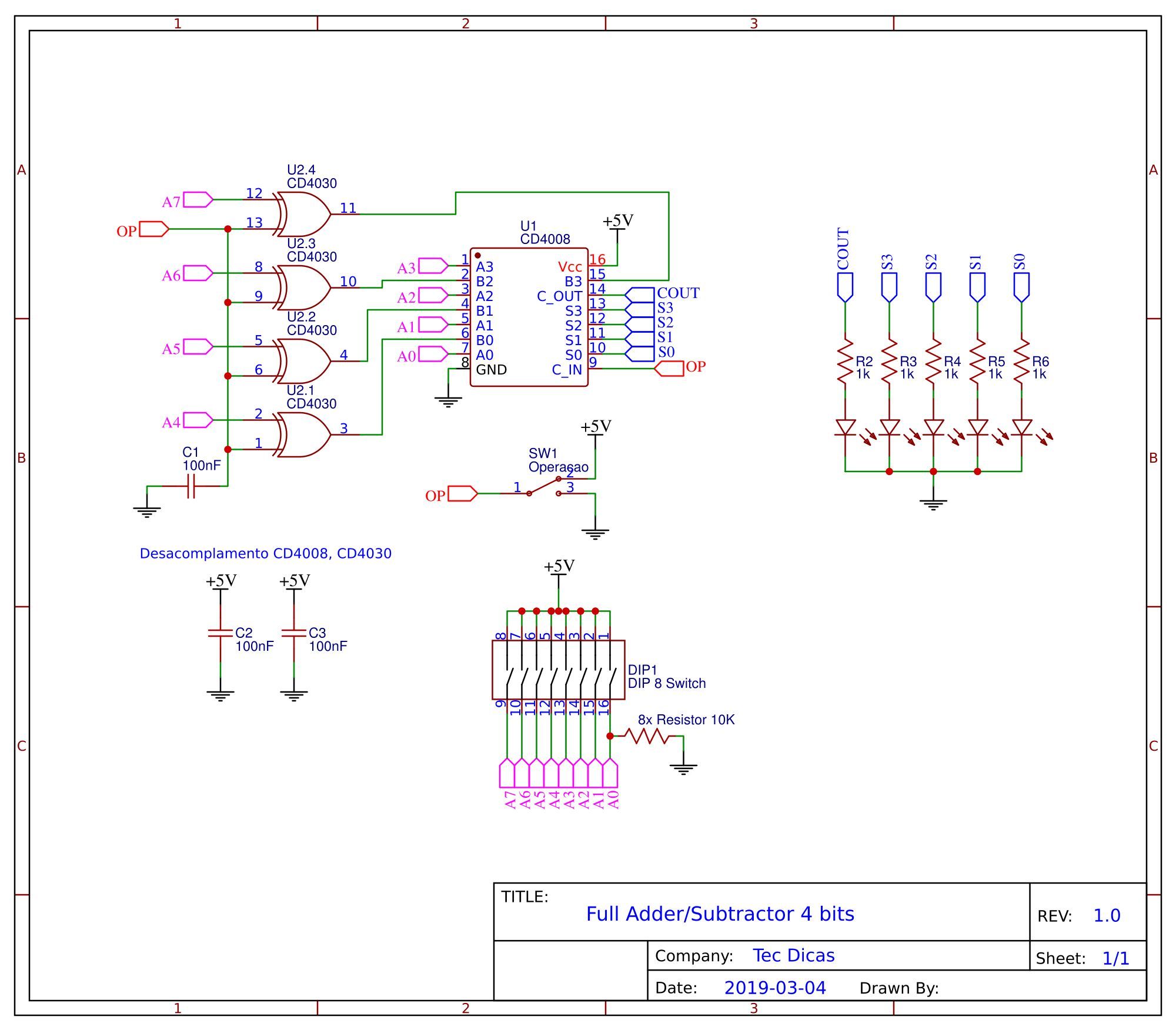
Com a montagem pronta no protoboard, podemos realizar diversas operações de adição e subtração com números binários. Configure a micro switch para o GND representando uma operação de adição, digite um número qualquer na repartição A do DIP switch, e depois na repartição B para gerar o resultado da adição automaticamente nos LEDs. Você pode mudar a micro switch para o 5V, realizando a operação de subtração dos mesmos números. Vale ressaltar que o bit de carry final da subtração é ignorado, e se o subtraendo é maior que o minuendo, teremos um número negativo em binário, como por exemplo, 0101 - 1010 = 1011 ou em hexadecimal FB.


Com este circuito podemos implementar displays de 7 segmentos para uma amostragem decimal dos resultados! Ficou interessado? Então leia o artigo Display decimal para circuito digital aritmético.
Referências
- MALVINO, A. P; BROWN, J. A; Digital computer electronics. 3 ed. McGraw-Hill, 1999.
- OSBORNE, A. Microprocessadores: conceitos básicos. 1 ed. São Paulo: McGraw-Hill, 1984.
- TOCCI, R, J; WIDMER, N. S; MOSS, G. L; Sistemas digitais: princípios e aplicações. 10 ed. Pearson Prentice Hall, 2008.