Os sistemas digitais são compostos pelas principais portas lógicas AND, OR, NOT e suas derivações. Independentemente da complexidade do circuito, podemos descrever a lógica utilizando as expressões booleanas de cada porta, obtendo facilmente a saída do circuito. Para iniciar o artigo, vamos aprender ou relembrar alguns conceitos importantes.
Álgebra booleana
A álgebra booleana nasceu de um estudo de George Boole, conhecido como "Uma investigação das leis de pensamento" onde o autor explana como tomar decisões lógicas baseando-se em situações verdadeiras ou falsas. Este método matemático expressa a relação entre as entradas e saídas de um circuito, utilizando letras como símbolos (A, B, C, D) para representar níveis lógicos, tendo como dois valores possíveis, o verdadeiro e falso. Comparando com a álgebra comum, a álgebra booleana é mais simples, pois trabalha com o sistema de numeração binário, não possui frações, raiz quadrada, números imaginários e nem logaritmos, e sim três operações lógicas elementares, a AND, OR e NOT, que dá vida às portas lógicas, tanto em teoria como prática.
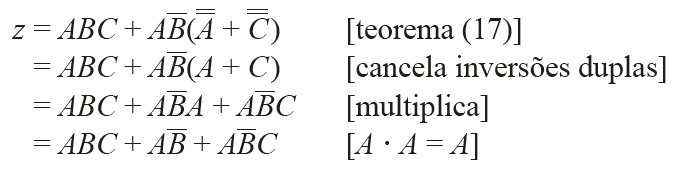
Mas qual a utilidade? Além da utilização como um instrumento de análise, a álgebra booleana é aplicada para simplificar expressões booleanas de um circuito utilizando teoremas (leis), onde a lógica é refinada e escrita novamente utilizando um número reduzido de portas lógicas e ligações, obtendo a mesma saída/resultado anterior.
A tabela verdade
A tabela verdade é um método para descrever como a saída de um circuito lógico se comporta com os níveis lógicos presentes nas entradas do circuito, oferecendo todas as combinações possíveis. Esta técnica é utilizada para documentar o projeto de circuitos lógicos combinacionais, e também utilizada para extrair as informações necessárias para uma expressão booleana.
As portas lógicas
Cada porta lógica possui o seu símbolo, tabela verdade e expressão booleana conforme imagem abaixo.
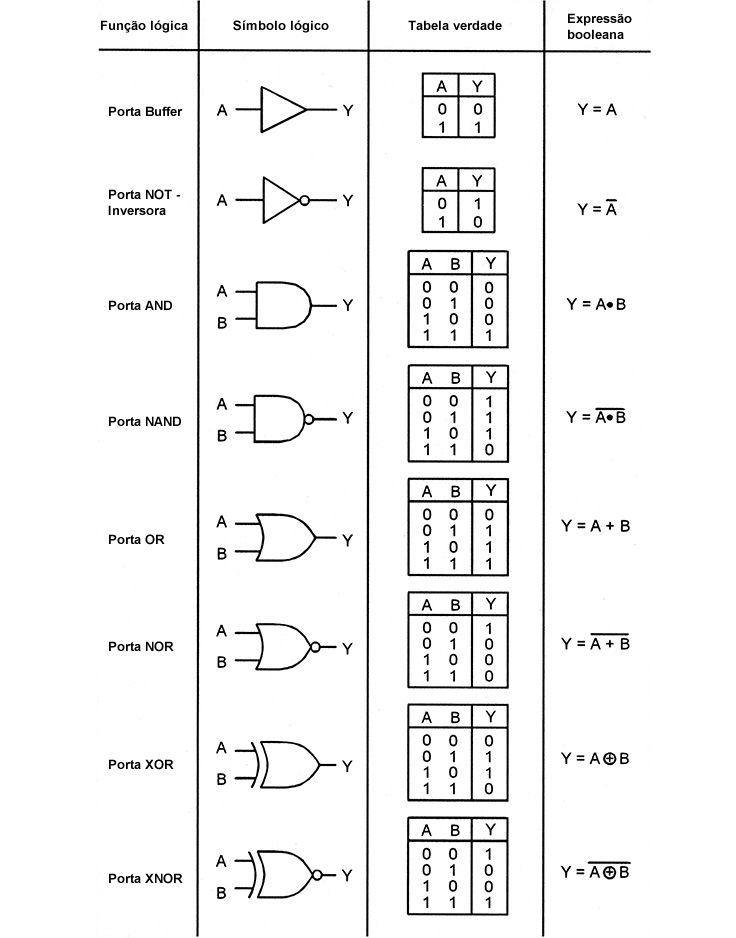
As principais portas lógicas e suas definições e aplicações reais, estão disponíveis no artigo Criando portas lógicas com transistores.
Com todos esses conceitos explanados, podemos descrever um circuito lógico algebricamente, utilizando símbolos lógicos, tabela verdade e expressões booleanas.
Desenvolvendo expressões booleanas
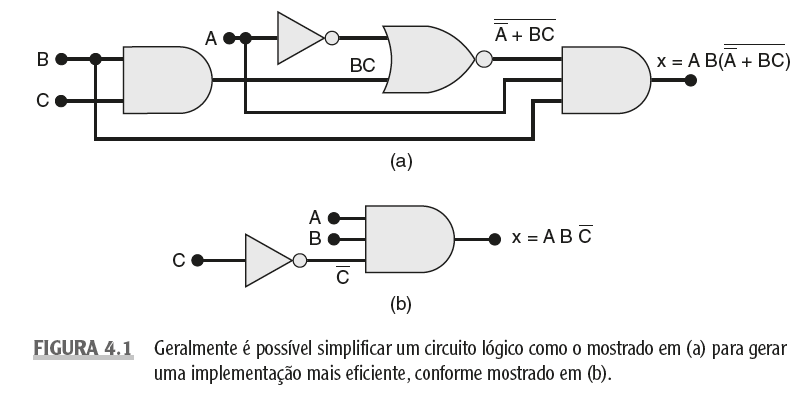
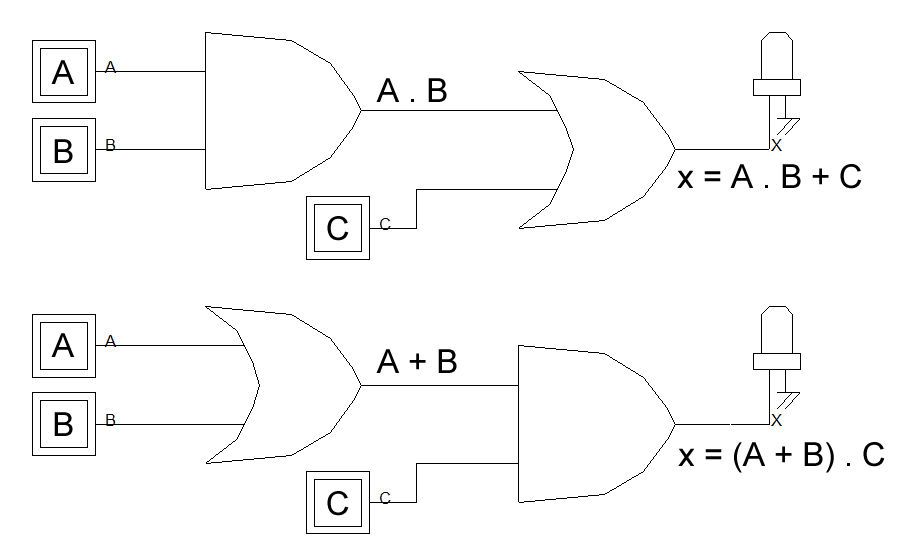
Podemos criar uma expressão booleana a partir de um circuito com portas lógicas para determinar sua saída. Observando a imagem abaixo, temos dois circuitos lógicos e suas expressões. No primeiro circuito, a expressão para a saída da porta AND é "A . B", ou "AB". Esta saída esta ligada em uma das entradas da porta OR, sendo a outra a C. A porta OR realiza a soma dos valores booleanos, obtendo a saída "x" deste circuito, onde "x = A . B + C".
No segundo circuito temos primeiramente a porta OR realizando a soma de "A + B", o resultado é conectado em uma das entradas da porta AND, sendo a outra a C. A porta AND realiza o produto dessas expressões, onde "x = (A + B) . C".
Em casos de dúvidas com o primeiro exemplo, sempre inicie a expressão com a lógica AND para evitar erros, pois esta expressão pode ser escrita também como "x = C + A . B". Porém quando temos em primeiro lugar uma porta OR utiliza-se parenteses, se a expressão fosse escrita "A + B . C", ela estaria sendo interpretada de forma incorreta, pois a operação de soma "A +" iria fazer parte do produto "B . C".
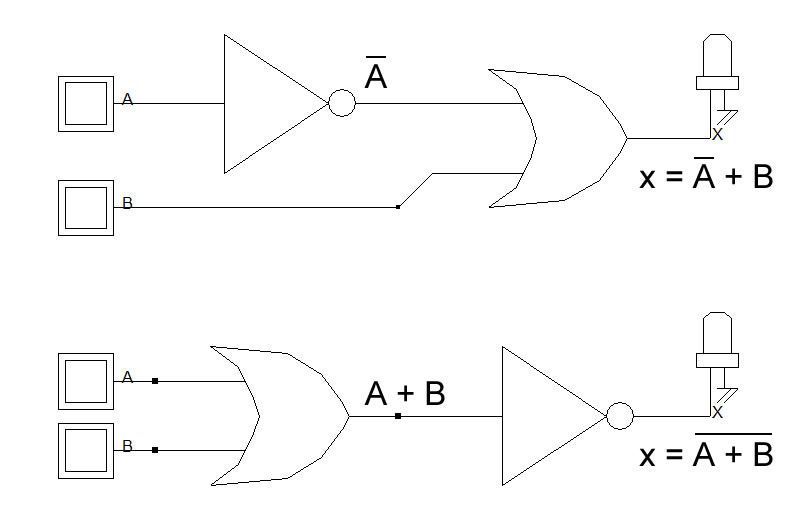
Quando um circuito possui uma porta lógica NOT ou inversora, a expressão de saída da NOT sempre será igual à expressão de entrada com uma barra encima, podemos ver esse exemplo da imagem abaixo. O valor booleano de A é invertido e é conectado em uma das portas da OR, sendo a outra a B, realizado a soma para obter a saída, onde "x = !A + B". No segundo circuito, temos primeiramente a porta OR realizando a soma de "A + B", entrando em uma porta NOT, realizando a inversão da soma. Vale ressaltar que no primeiro circuito, somente A é invertido, e B não, e no segundo circuito ambas entradas são invertidas.
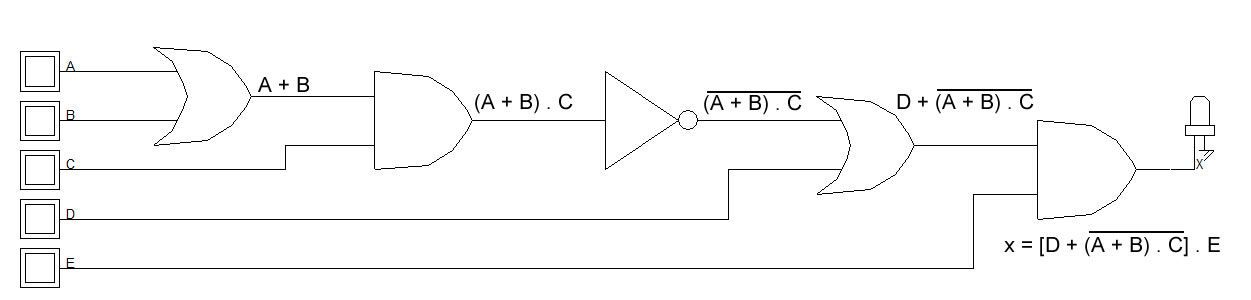
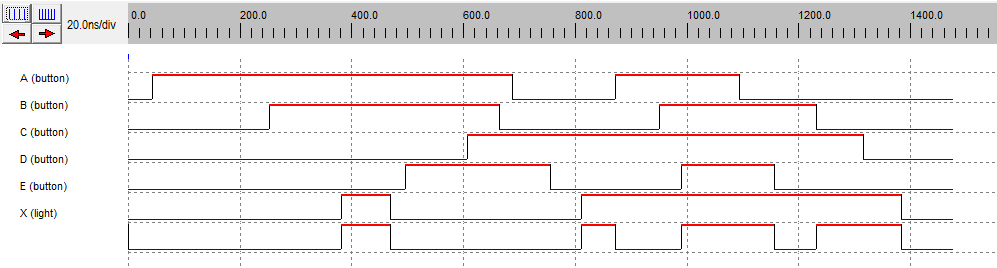
Este outro circuito é um pouco diferente, ele possui cinco portas lógicas com suas entradas de "A, B, C, D, E" e sua saída é bem interessante, pois possui parenteses e colchetes. A Figura 8a representa o diagrama de tempo do circuito, onde podemos observar os sinais retangulares dos níveis lógicos em uma simulação realizada no software Dsch3.
Utilizando a expressão booleana final do circuito acima, podemos realizar uma substituição das letras A, B, C, D, E das entradas com níveis lógicos para conhecer o estado da saída. O método é semelhante com a álgebra comum, onde substituímos os valores das variáveis para conhecer o resultado de "X".
Temos, A = 0 , B = 0, C = 1, D = 1 e E = 1,
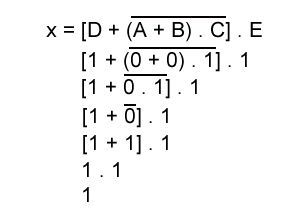
Para realizar passo a passo desta expressão booleana conforme a imagem acima, precisamos seguir quatro regras importantes citadas por TOCCI e seus colegas, onde:
- Primeiro, realize as inversões de termos simples; ou seja, 0 = 1 ou 1 = 0.
- Em seguida, realize as operações dentro de parênteses.
- Realize as operações AND antes das operações OR, a menos que os parênteses indiquem o contrário.
- Se uma expressão tiver uma barra sobre, realize a operação indicada pela expressão e, em seguida, inverta o resultado.
Após todos esses exemplos de como descrever um circuito lógico algebricamente, podemos montar uma tabela verdade a partir de um circuito lógico, e depois realizar o procedimento de descrever a expressão booleana e simplificá-la utilizando os teoremas básicos da álgebra booleana.
Analisando uma tabela verdade
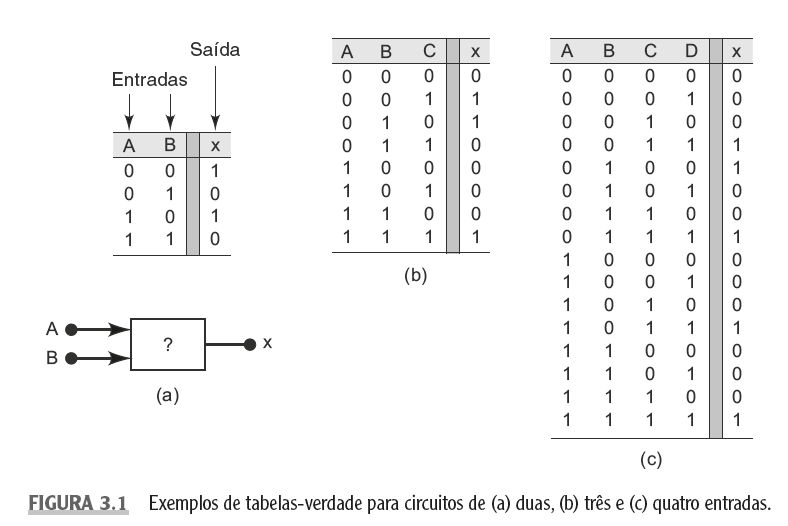
Para saber como um circuito lógico funciona com todas as possíveis possibilidades, podemos utilizar uma tabela verdade, pois ela permite uma análise minuciosa da lógica, além de possuir uma tabela documentada para consultas posteriores.
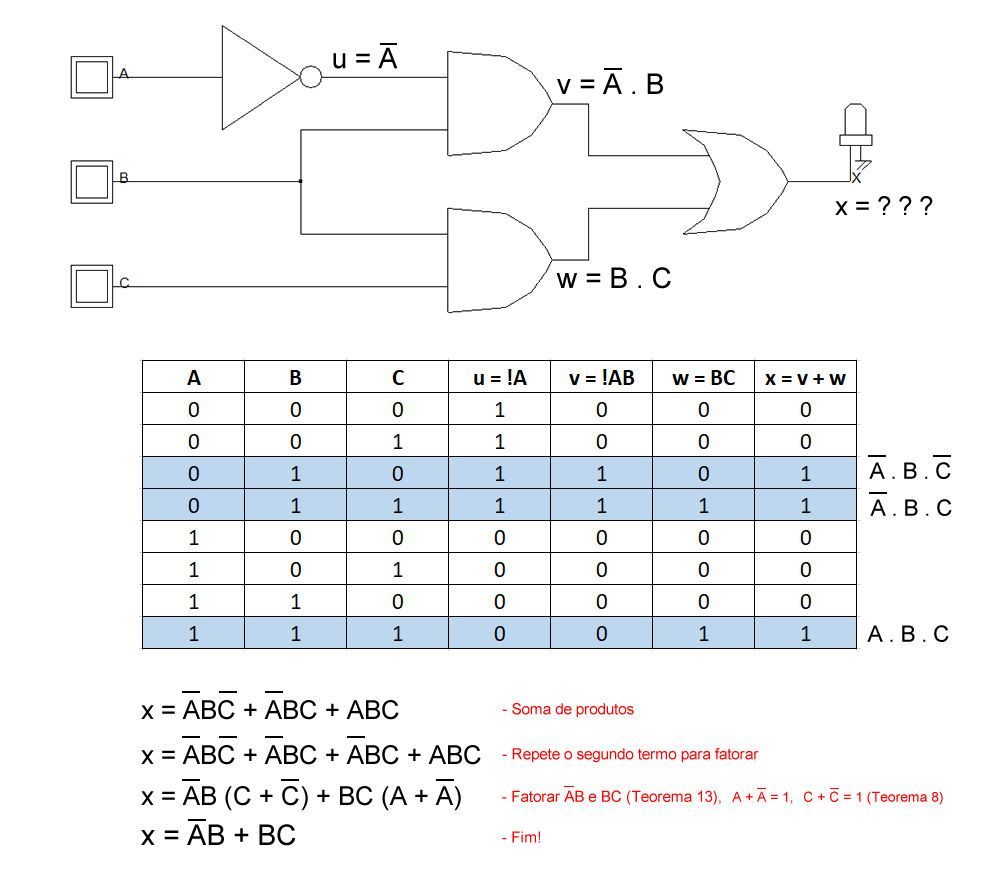
Observando a imagem abaixo, temos um circuito com portas lógicas e três entradas A, B e C, onde a saída "X" é desconhecida. Para descobrir o comportamento deste circuito, é necessário implementar uma tabela verdade, adicionando as entradas, as portas lógicas e a saída conforme o diagrama do circuito. Com a tabela completa, separamos todas as saídas que são verdadeiras ou 1, e escrevemos algebricamente seus produtos e somas. Todas as linhas da tabela com saídas verdadeiras são descritas como um produto, "A . B . C", e a junção destes produtos são realizadas com uma soma, onde "A . B . C + A . B . C...". conhecido como "expressão booleana em forma de soma-de-produtos".
Com a expressão booleana completa, podemos aplicar a álgebra booleana para simplificar este resultado. Conforme a expressão abaixo, utilizamos os teoremas 13 e 8, podendo aplicar a fatoração dos termos, onde as somas de A e !A, C e !C são igual à um, anulando esses termos da expressão. Com esses simples passos, reduzimos a expressão booleana alcançando a mesma lógica do circuito proposto.
Desafios!
Para você que gosta de eletrônica digital, separamos alguns desafios para praticar ainda mais.
- Utilizando o circuito da Figura 8, troque as portas AND por OR e cada porta OR por AND. E depois escreva a expressão booleana da saída "X".
- Faça o diagrama de tempo da Figura 10 utilizando as informações da tabela verdade.
Referência
- TOCCI, R, J; WIDMER, N. S; MOSS, G. L; Sistemas digitais: princípios e aplicações. 11 ed. Pearson Prentice Hall, 2011.