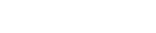Introdução
Para iniciar este artigo é importante salientar que as máquinas em seu interior não sabem interpretar números decimais (5, 12, 20, 32) por suas condições elétricas, por este motivo que a lógica binária é adotada. O sistema de numeração binário é composto por dois números, sendo 0 ou 1. Eles representam estados de ligado/verdadeiro e desligado/falso, tornado-se aplicável em relés e transistores de junção bipolar, componentes que deram vida aos primeiros computadores. Estes componentes comuns da eletrônica se comportam como um circuito digital, pois entregam a característica de mudanças de estados, representados por variações de níveis de tensões, no qual os intervalos são de 0-0,8 Volts para falso e 2-5 Volts para verdadeiro.
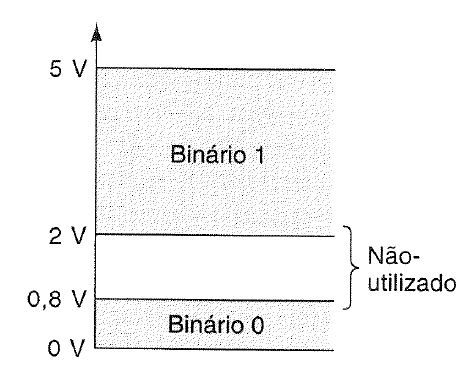
Quando este tipo de circuito é capaz de responder a uma ou várias entradas de dados, chamamos ele de circuito lógico. que são capazes de interpretar diversas operações lógicas ou booleanas, como as portas lógicas E, OU, INVERSORA e suas derivações. Podemos desenvolver circuitos com diversas portas lógicas combinadas para gerar um resultado satisfatório em uma determinada função do sistema. Em projetos eletrônicos reais utilizamos estas portas lógicas encapsuladas em CIs - Circuitos Integrados, sendo mais práticos no dia a dia. Quando uma lógica combinacional ou sequencial é muito difundida entre os projetistas, elas seguem o mesmo processo de encapsulamento, favorecendo cada vez mais a miniaturização dos circuitos.
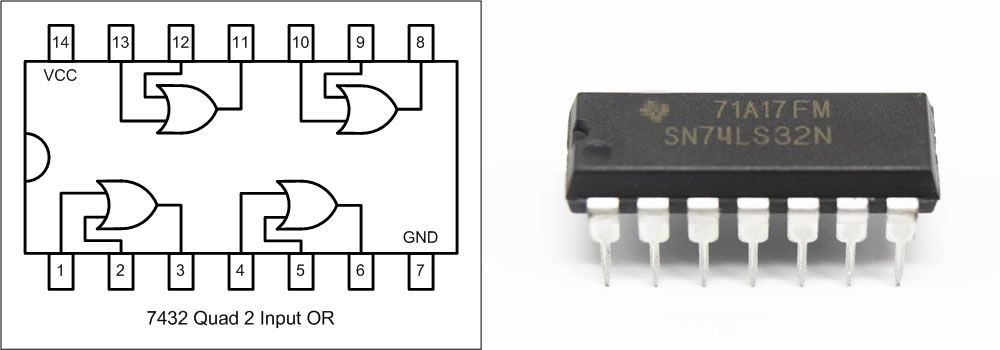
Você já se perguntou como os computadores e calculadoras realizam a operação aritmética mais simples de todas? Para realizar uma soma decimal precisamos de dois números, por exemplo 10 e 2, e depois somar estes números para obter um resultado, onde 10 + 2 = 12. A adição binária não é diferente, porém utilizamos números decimais convertidos para a base binária. Para realizar o cálculo utilizamos um conjunto de 4 bits ou nibble, ou seja, 10 em binário é 1010 e 2 é 0010, somando estes números teremos 1010 + 0010 = 1100.
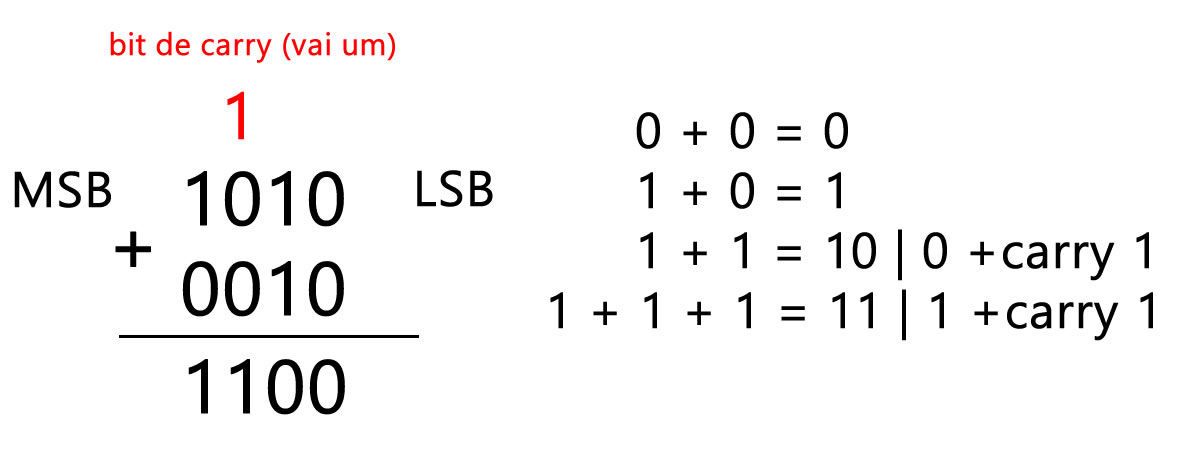
Vamos realizar estes passos detalhadamente no "papel", a adição binária se inicia sempre pelo bit menos significativo ou LSB, então começando a operação temos 0 + 0 = 0, qualquer lógica comum que possui as entradas em 0 o resultado será 0, exceto quando trabalhamos com a porta lógica Inversora/NOT e suas derivadas. Depois realizamos 1 + 1 = 10, como este valor possui dois números binários, o 1 é o bit de carry ou "vai um" da adição tradicional. Agora temos o bit de carry, então somamos ele 1 + 0 + 0 = 1, e finalmente temos 1 + 0 = 1, chegando em nosso resultado final de 1100 ou 12 na base decimal. Você pode treinar a adição binária com outros valores, se tiver dúvidas do resultado utilize a calculadora do Windows em modo Programador.
Esse é o método teórico que os computadores e calculadoras realizam a adição, mas como somar números binários em um circuito real?
Foi desenvolvido para este artigo um circuito combinacional com portas lógicas, capaz de realizar a operação aritmética de adição de 4 bits, explanando um nível baixo de abstração digital.
Importante: Para acompanhar e absorver o conteúdo deste artigo, é necessário estudar ou relembrar alguns conceitos básicos da eletrônica digital. No artigo Criando portas lógicas com transistores, foi abordado as principais portas lógicas e suas características utilizando transistores. E no artigo Prática de circuitos combinacionais e sequenciais, ensina como construir circuitos lógicos combinacionais e sequenciais utilizando CIs.
Full Adder
Full Adders ou Somadores completos é a lógica combinacional para somar números binários na eletrônica digital. Os computadores e calculadoras possuem este circuito, porém embutido na Unidade Aritmética do microprocessador, que realizam operações binárias mais complexas derivadas de Full Adders, como subtração, divisão e multiplicação.
O circuito é composto por portas lógicas E/AND, OU/OR e OU EXCLUSIVO/XOR, como mostra a imagem abaixo de um Full Adder de 1 bit com carry out. Com este circuito você pode somar até 2 ou 0010.
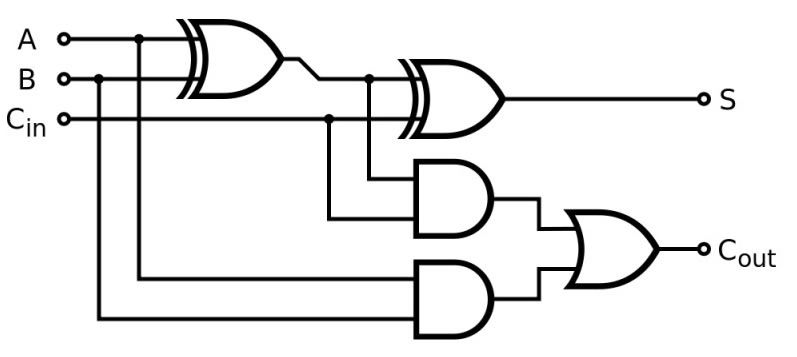
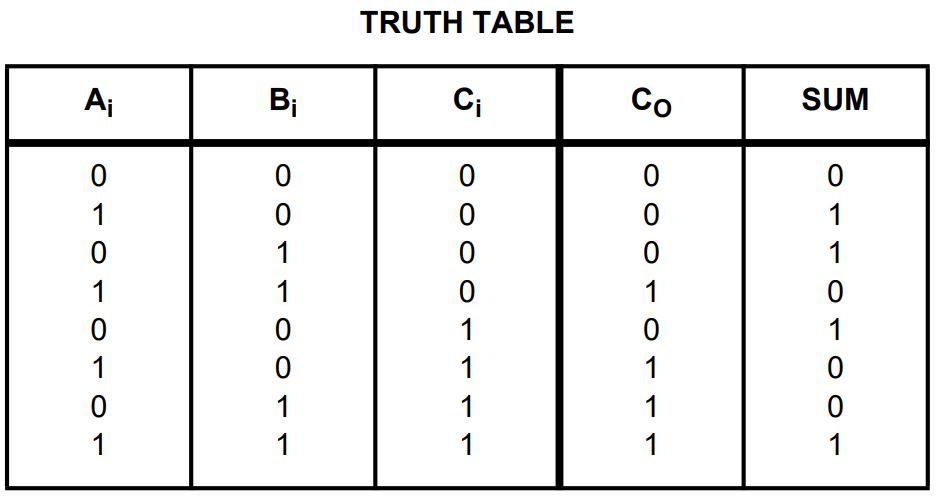
O funcionamento deste circuito não tem segredo, as entradas A, B são os valores que queremos somar, Cin é o bit de carry, onde o primeiro é zero ou GND para representar uma adição. As saídas S e Cout representam o resultado da adição, onde Cout é o "estouro" da operação, onde podemos analisar esses valores utilizando a sua tabela verdade. Para somar 4 bits são necessários quatro destes circuitos em cascata, onde o primeiro Cout é ligado no segundo Cin e assim por diante, aumentando o resultado para 30 ou 11110!
Agora podemos iniciar a montagem do Full Adder de 4 bits no protoboard, para isso separamos uma lista de materiais necessários.
- 1 Protoboard
- 2 CIs 7486 ou CD4030 (Quad two-input XOR gate)
- 2 CIs 7408 (Quad two-input AND gate)
- 1 CI 7432 (Quad two-input OR gate)
- 1 DIP switch de 8 posições ou 2 DIPs de 4 posições
- 8 Resistores de 1K
- 5 Capacitores de poliéster/cerâmico de 100nF
- 5 LEDs, de preferencia um LED com cor diferente para carry out
- Fios jumpers
- Fonte de alimentação 5V ou módulo fonte de alimentação para protoboard.
Com os materiais em mãos, siga o diagrama esquemático abaixo do Full Adder de 4 bits.
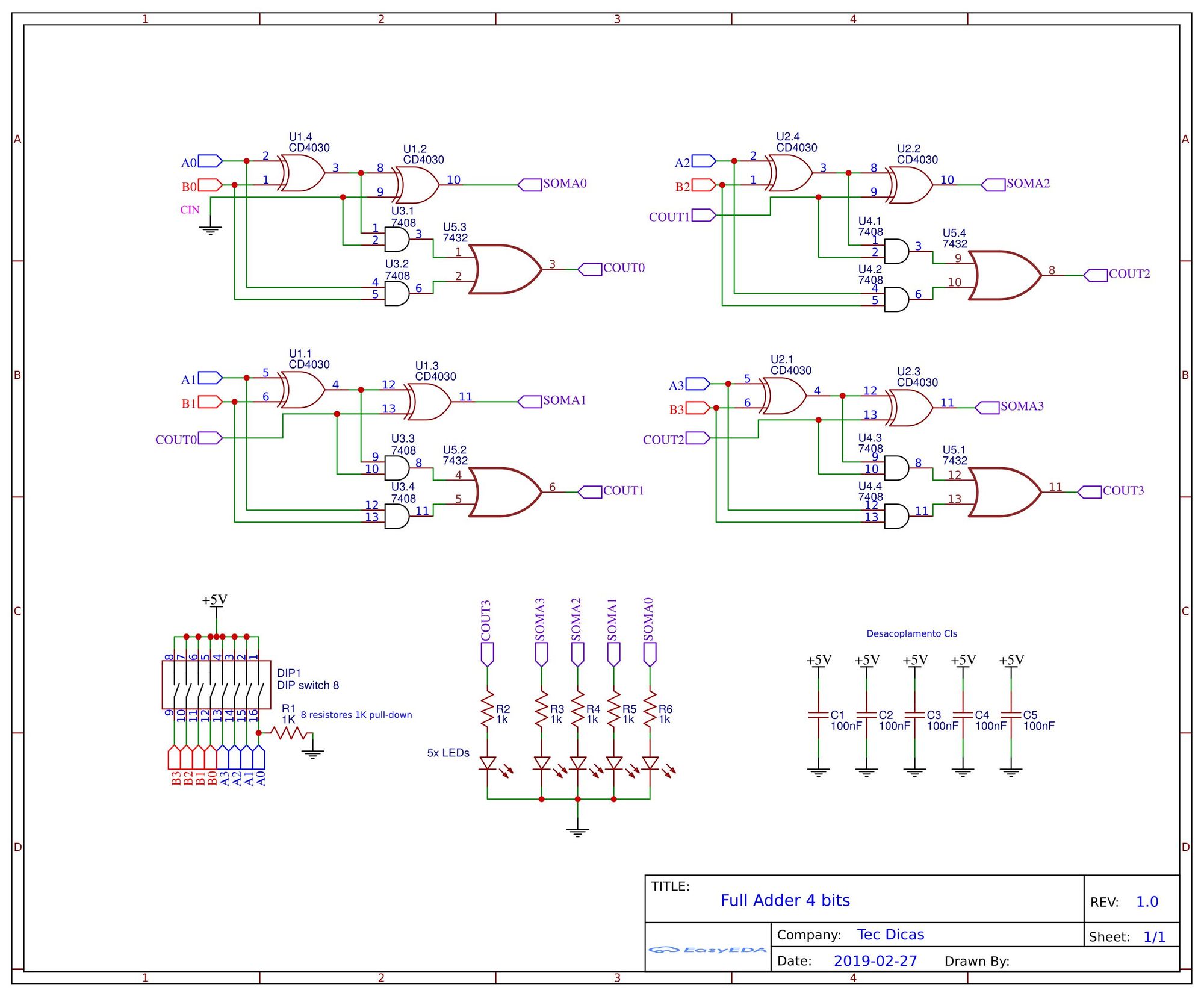
A montagem no protoboard deve ficar semelhante a imagem abaixo.

Como a lógica de Full Adder é comum, montar este circuito com cinco CIs toda vez que for necessário é extremamente trabalhoso, então para economizar tempo e reutilizar sempre a mesma lógica, existem Full Adders de 4 bits encapsulados em um único CI. Podemos utilizar os CIs CD4008 (CMOS 4-Bit Full Adder With Parallel Carry Out) ou 74283 (TTL 4-Bit Binary Adder with Fast Carry). As aplicações utilizando esses CIs são inúmeras, uma delas é realizar a operação aritmética de subtração adicionando novos componentes à lógica do circuito.
Referências
- MALVINO, A. P; BROWN, J. A; Digital computer electronics. 3 ed. McGraw-Hill, 1999.
- OSBORNE, A. Microprocessadores: conceitos básicos. 1 ed. São Paulo: McGraw-Hill, 1984.
- TOCCI, R, J; WIDMER, N. S; MOSS, G. L; Sistemas digitais: princípios e aplicações. 10 ed. Pearson Prentice Hall, 2008.